הסטוריה קצרה על פיי

תכונות

π הוא מספר אי רציונלי, כלומר אינו ניתן לכתיבה כיחס בין שני מספרים שלמים. תכונה זו הוכחה בשנת 1761 על ידי יוהן היינריך למברט.

בשנת 1882 הוכיח פרדיננד לינדמן ש-π הוא מספר טרנסצנדנטי. מהוכחה זו נובע ש-π אינו ניתן להצגה תוך שימוש במספר סופי של מספרים שלמים, שברים או שורשים שלהם. כתוצאה מהוכחה זו נובע שלא ניתן, באמצעות בנייה בסרגל ומחוגה לבנות ריבוע השווה בשטחו לעיגול נתון.

חישוב π

חישוב ערך מדויק יותר ויותר של π היווה אתגר במשך מאות שנים.

בספר מלכים א' (ז, כג) יש רמז ל- π :"ויעש את הים מוצק עשר משפתו על שפתו עגול סביב וחמש באמה קומתו וקוה שלושים באמה וסוב אותם סביב". חישוב פשוט לפי פסוק זה נותן ל- π את הערך 3, שהוא קירוב גרוע ביותר של π (פרשנים ניסו להסביר תוצאה זו, כך שתיראה טוב יותר, למשל בהסבר שמדובר בקוטר חיצוני ובהיקף פנימי, או בהסבר מתוחכם יותר (http://www.cs.biu.ac.il/~tsaban/Pdf/exactpi.pdf)).

צורת השבר הפשוטה ביותר המקרבת את π, היא 22/7 או 1/7 3. קירוב מקובל של π כמספר עשרוני הוא 3.14 . קירובים אלה מתלכדים עם ערכו האמיתי של π בדיוק של שתי ספרות בלבד מימין לנקודה.

ארכימדס הציג לראשונה שיטה המאפשרת לחשב את π בכל רמת דיוק שתידרש. שיטתו מתבססת על כך שהיקף המעגל קטן מהיקפו של מצולע החוסם את המעגל וגדול מהיקפו של מצולע החסום במעגל. באמצעות חישוב ההיקף של מצולע חוסם ומצולע חסום בעלי מספר הולך וגדל של צלעות נשיג דיוק גדל והולך של היקף המעגל, ובהתאם לכך דיוק גדל והולך של π. ארכימדס הפעיל את שיטתו על משושה, ובהדרגה הכפיל את מספר הצלעות. מצולע בן 96 צלעות הביא את ארכימדס לתוצאה

. 3 1/7 > π > 3 10/71

(http://www.math.utah.edu/~alfeld/Archimedes/Archimedes.html)

דיוק בן שבע ספרות הושג במאה ה-16 על-יד ההולנדי אדריאן אנטוניזון, שהציג את π באמצעות השבר 355/113. קל לזכור שבר זה, המורכב משלושת המספרים האיזוגיים הראשונים, שכל אחד מהם נרשם פעמיים, וקו שבר חוצה את שש הספרות באמצען.

בשנת 1596 השתמש ההולנדי לודולף ואן צאולן בשיטתו של ארכימדס, וחישב את π בדיוק של 20 ספרות, וכעבור שנים אחדות הגיע לדיוק של 35 ספרות. הוא היה כל כך גאה בהישג זה, עד שציווה לכתוב ספרות אלה על מצבתו. גם הגרמנים התרשמו מאוד מהישג זה, וקראו ל-π בשם מספר לודולף.

התפתחות החשבון האינפיניטסימלי במאה ה-17 הביאה שיטות חדשות לחישובו של π, שיטות המתבססות על ייצוגו של π כסכום של טור אינסופי.

בשנת 1789 חישב הסלובני יורי וגה את 140 הספרות הראשונות של π (רק 137 מתוכן היו נכונות).

השתכללות המחשבים ומציאת אלגוריתמים יעילים יותר לחישובו של π הביא לשיא הנוכחי (שנוצר בספטמבר 2002) - חישוב 1,241,100,000,000 ספרות, באמצעות מחשב-על מתוצרת היטאצ'י. מובן שלתוצאה זו אין כל ערך מעשי, מלבד הפגנת מהירותם של מחשבי-על ושל אלגוריתמים.

מי שמשתוקק לקבל ספרות רבות מספור של π מוזמן לדלג לאתר הבא:

3.141592653589793238462643383279502884197169399375105820974944592

טכניקה לא שגרתית לחישובו של π היא "שיטת מונטה-קרלו": על לוח עץ נצייר ריבוע שאורך צלעו שתי יחידות. נצייר מעגל חסום בריבוע זה (זהו מעגל שרדיוסו שווה ליחידה אחת), ונתחיל להטיל חיצים אל הריבוע (לא נכוון את החץ למרכז הריבוע, אלא אל הריבוע כולו, באופן אקראי). לאחר מספר רב של הטלות, היחס בין מספר הפעמים שהחצים פגעו בתוך המעגל, למספר הפעמים שבהם פגעו בתוך הריבוע שואף ליחס שבין שטחי שתי הצורות, שהוא 4 / π .

נוסחאות הקשורות ב-π

פאי מופיע בנוסחאות מתמטיות רבות. ניתן לצפות שיופיע בנוסחאות הקשורות לשטחי ונפחי צורות מעגליות, שכן הוא מוגדר באמצעות מעגל, אך לעתים הוא מתגלה גם בתחומים שלכאורה אין בינם ובין גיאומטריה או מעגלים קשר ישיר.

גיאומטריה


היקף מעגל	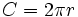$C = 2 \pi r \,\!$
שטח מעגל	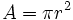$A = \pi r^2 \,\!$
שטח של אליפסה	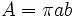$A = \pi a b \,\!$
נפח של כדור	$V = \frac{4}{3} \pi r^3 \,\!$
שטח פנים של כדור	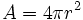$A = 4 \pi r^2 \,\!$
נפח של גליל	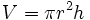$V = \pi r^2 h \,\!$
שטח פנים של גליל	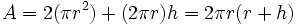$A = 2 ( \pi r^2 ) + ( 2 \pi r ) h = 2 \pi r (r + h) \,\!$
נפח של חרוט	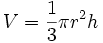$V = \frac{1}{3} \pi r^2 h \,\!$
שטח פנים של חרוט	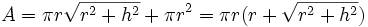$A = \pi r \sqrt{r^2 + h^2} + \pi r^2 = \pi r (r + \sqrt{r^2 + h^2}) \,\!$

אנליזה מתמטית

נוסחת פרנסואה ויאטה, 1593:

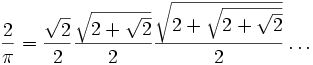
$\frac2\pi= \frac{\sqrt2}2 \frac{\sqrt{2+\sqrt2}}2 \frac{\sqrt{2+\sqrt{2+\sqrt2}}}2\ldots$

נוסחת לייבניץ:

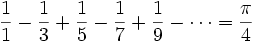
$\frac{1}{1} - \frac{1}{3} + \frac{1}{5} - \frac{1}{7} + \frac{1}{9} - \cdots = \frac{\pi}{4}$

ובכתיב כללי יותר:

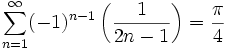
$\sum_{n=1}^{\infty} (-1)^{n-1} \left (\frac{1}{2n-1}\right ) = \frac{\pi}{4}$

מכפלת ואליס:

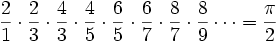
$\frac{2}{1} \cdot \frac{2}{3} \cdot \frac{4}{3} \cdot \frac{4}{5} \cdot \frac{6}{5} \cdot \frac{6}{7} \cdot \frac{8}{7} \cdot \frac{8}{9} \cdots = \frac{\pi}{2}$

נוסחת אינטגרל מהחשבון האינפיניטסימלי (הקשורה בהסתברות).

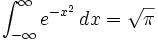
$\int_{-\infty}^{\infty} e^{-x^2}\,dx = \sqrt{\pi}$

בעיית בסל נפתרה לראשונה על-ידי לאונרד אוילר (ראו גם פונקציית הזטה של רימן):

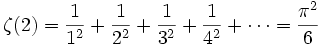
$\zeta(2) = \frac{1}{1^2} + \frac{1}{2^2} + \frac{1}{3^2} + \frac{1}{4^2} + \cdots = \frac{\pi^2}{6}$

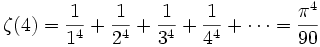
$\zeta(4)= \frac{1}{1^4} + \frac{1}{2^4} + \frac{1}{3^4} + \frac{1}{4^4} + \cdots = \frac{\pi^4}{90}$

פונקציית גאמה (המהווה הכללה של פונקציית העצרת) בנקודה 1/2:

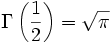
$\Gamma\left({1 \over 2}\right)=\sqrt{\pi}$

נוסחת סטירלינג המשמשת לקירוב עצרת של מספרים גדולים:

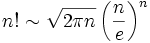
$n! \sim \sqrt{2 \pi n} \left(\frac{n}{e}\right)^n$

נוסחת אוילר (שנקראה על ידי ריצ'רד פיינמן "הנוסחה המופלאה ביותר במתמטיקה", ומקשרת בין חמשת הקבועים המתמטיים הבסיסיים):

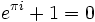
$e^{\pi i} + 1 = 0\;$

שטחו של רבע מעיגול היחידה:

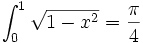
$\int_0^1 \sqrt{1-x^2} = {\pi \over 4}$

אנליזה מרוכבת

יישום של משפט השאריות:

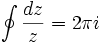
$\oint\frac{dz}{z}=2\pi i$

שברים משולבים

אפשר להציג את פאי באמצעות שברים משולבים רבים, בינהם:

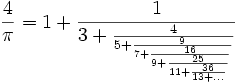
$\frac{4}{\pi} = 1 + \frac{1}{3 + \frac{4}{5 + \frac{9}{7 + \frac{16}{9 + \frac{25}{11 + \frac{36}{13 + ...}}}}}}$

תורת המספרים

בתורת המספרים יש קשר בין פאי לבין מספר תוצאות:

ההסתברות ששני מספרים אקראיים יהיו מספרים זרים הוא 6/π².
ההסתברות שמספר אקראי יהיו מספר לא רבוע הוא 6/π².
מספר הדרכים הממוצע שבהן ניתן לכתוב מספר טבעי כסכום של שני מספרים ריבועיים הוא π/4.

כאן אנו מניחים שההסתברות והממוצע נלקחים על קבוצת המספרים הטבעיים עד N, כאשר N שואף לאינסוף.

פיסיקה

נוסחאות בפיסיקה.

עקרון אי הוודאות:

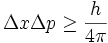
$\Delta x \Delta p \ge \frac{h}{4\pi}$

משוואת השדה של איינשטיין בתורת היחסות הכללית:

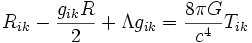
$R_{ik} - {g_{ik} R \over 2} + \Lambda g_{ik} = {8 \pi G \over c^4} T_{ik}$

חוק קולון לגבי כוח חשמלי:

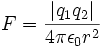
$F = \frac{\left|q_1q_2\right|}{4 \pi \epsilon_0 r^2}$

הפולקלור של π

קיימים משפטים שונים המסייעים ללימוד בעל-פה של π, בכך שמספר האותיות בכל מלה שלהם שווה לספרה המתאימה של π. המפורסם שבהם הוא של אייזיק אסימוב:

How I want a drink, alcoholic of course, after the heavy lectures involving quantum mechanics!

יש החוגגים את ה-14 במרץ (שנרשם כ-3.14) כיום π, ואחרים חוגגים זאת ב-22 ביולי (הוא 22/7).

חמשירים אחדים חוברו לכבודו של פאי, הנה אחד מהם:

'Tis a favorite project of mine
A new value of pi to assign.
I would fix it at 3
For it's simpler, you see,
Than 3 point 1 4 1 5 9 !

חזרה